Understanding Positional Encoding in AI
(FIXED POSITIONAL EMBEDDINGS)
Understanding Embeddings and Absolute Positional Embeddings in NLP
1. Introduction to Embeddings
Embeddings are a crucial concept in Natural Language Processing (NLP), acting as a bridge between human language and machine understanding. They transform discrete objects, such as words or tokens, into continuous vectors of numbers within a high-dimensional space.
Why Do We Need Embeddings?
Machine Comprehension: Computers cannot directly process words or symbols; embeddings convert human language into a machine-readable format.
Efficient Processing: Vector representations facilitate fast and efficient computations on large text datasets.
Semantic Relationships: Embeddings capture the meanings and relationships between words mathematically.
Types of Embeddings:
Word Embeddings: Represent individual words or tokens.
Sentence Embeddings: Capture the meaning of entire sentences.
Document Embeddings: Represent whole documents or paragraphs.
Cross-modal Embeddings: Represent data from different modalities (e.g., text and images) in a shared space.
2. Word Embeddings
Word embeddings encode the meanings of words based on their contexts. They enable models to understand semantic similarities and relationships effectively.
Dimensionality of Word Embeddings: The dimensionality (embedding size) of word embeddings is typically set based on the model's architecture and can vary widely. Common sizes include:
50 dimensions: Often used in simpler models.
100 dimensions: A balance between complexity and performance.
300 dimensions: Commonly used in advanced embeddings like Word2Vec and GloVe for richer semantic representation.
Training Methods: Word embeddings are typically trained using unsupervised methods on large text corpora. Popular algorithms include:
Word2Vec: Uses skip-gram or continuous bag-of-words (CBOW) approaches to predict context words from target words or vice versa.
GloVe (Global Vectors for Word Representation): Utilizes word co-occurrence statistics to learn embeddings.
FastText: Extends Word2Vec by representing words as bags of character n-grams, allowing it to generate embeddings for out-of-vocabulary words.
Example: Visualizing Word Embeddings
Here’s a Python code snippet to visualize word embeddings using t-SNE:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
# Sample text
sample_text = "The cat sat on the mat. The dog barked at the moon."
words = sample_text.lower().replace('.', '').split()
vocab = list(set(words)) # Unique words in the text
# Create one-hot encodings for each word
one_hot_encodings = np.eye(len(vocab))
# Simulate word embeddings by projecting one-hot vectors into a random 50D space
np.random.seed(42)
embedding_dim = 50
word_embeddings = np.dot(one_hot_encodings, np.random.rand(len(vocab), embedding_dim))
# Reduce dimensionality to 2D using t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=5)
reduced_embeddings = tsne.fit_transform(word_embeddings)
# Plot the word embeddings
plt.figure(figsize=(8, 6))
plt.scatter(reduced_embeddings[:, 0], reduced_embeddings[:, 1], color='blue')
for i, word in enumerate(vocab):
plt.text(reduced_embeddings[i, 0], reduced_embeddings[i, 1], word, fontsize=12)
plt.title("Word Embeddings Visualization (t-SNE)")
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.grid(True)
plt.show()
The embeddings are random in this example and that meaningful relationships would emerge with trained embeddings.
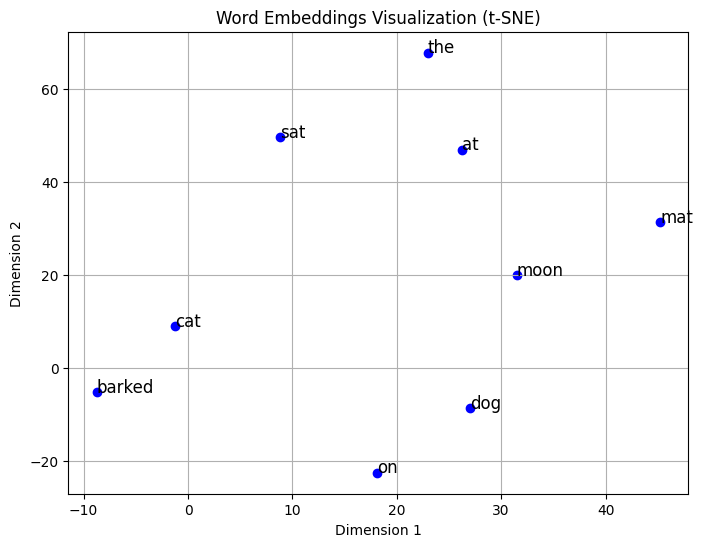
Word Embeddings Visualization (t-SNE plot): This plot shows how the words from your sample sentence "The cat sat on the mat. The dog barked at the moon." are arranged in a 2D space after dimensionality reduction using t-SNE. Here's what we can observe:
Related words are positioned closer together. For example:
"cat" and "dog" are somewhat close to each other since they're both animals
"sat" and "at" share similar positions, possibly due to their usage as position/action words
"mat" and "moon" are far apart, which makes sense as they're semantically different
Words like "the" and "on" appear in distinct locations, reflecting their unique roles as function words
The distances between points represent the model's understanding of semantic relationships between words, though in this simple example with random embeddings, these relationships are not as meaningful as they would be in a properly trained word embedding model like Word2Vec.
Key Characteristics of Word Embeddings:
Capture semantic relationships between words.
Do not encode sequential information; for example, "The cat sat on the mat" and "Mat on sat cat the" would have identical embeddings.
3. Absolute Positional Embeddings
Absolute positional embeddings are essential in Transformer-based models and it was first introduced in the paper Attention is all you need, allowing them to understand the sequential nature of language.
The Formula
The formula for absolute positional embeddings uses sine and cosine functions:
Where:
pos is the position of the token in the sequence.
i is the dimension index.
d_model is the dimensionality of the model.
Handling Position Awareness: In Transformer models, which lack recurrence (as seen in RNNs), there is no inherent way to capture the order of tokens. Absolute positional embeddings provide explicit positional information that allows models to differentiate between tokens based on their positions within a sequence.
Properties of Absolute Positional Embeddings:
Handle variable-length sequences.
Allow models to attend to relative positions easily.
Values are bounded between -1 and 1, preventing issues with large numbers.
Methods of Implementation:
Fixed (Sinusoidal) Approach:
Generates fixed positional encodings using the above formula.
Advantages include no additional parameters to learn and handling longer sequences than seen during training.
def get_sinusoidal_positional_encoding(max_seq_len, d_model):
position = np.arange(max_seq_len)[:, np.newaxis]
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe = np.zeros((max_seq_len, d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
Limitation of Sinusoidal Positional Embeddings: While sinusoidal embeddings have advantages like interpolation capabilities, they are limited in their ability to generalize to sequences longer than those seen during training. This limitation has led some models (e.g., T5) to adopt learned positional embeddings instead.
Learned Approach:
Positional embeddings are learned during training, similar to word embeddings.
Advantages include capturing more complex positional relationships tailored to specific datasets.
import torch.nn as nn
class LearnedPositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=512):
super().__init__()
self.positional_embedding = nn.Embedding(max_len, d_model)
def forward(self, x):
positions = torch.arange(x.size(1), device=x.device).unsqueeze(0)
return self.positional_embedding(positions)
Visualization: Heatmap of Positional Embeddings
import seaborn as sns
# Define a function to generate sinusoidal positional embeddings
def get_positional_encoding(max_seq_len, d_model):
position = np.arange(max_seq_len)[:, np.newaxis] # Sequence positions (rows)
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model)) # Scaling factor
pos_encoding = np.zeros((max_seq_len, d_model))
pos_encoding[:, 0::2] = np.sin(position * div_term) # Sine for even indices
pos_encoding[:, 1::2] = np.cos(position * div_term) # Cosine for odd indices
return pos_encoding
# Generate positional embeddings for the sample text
max_seq_len = len(words) # Number of words in the sample text
d_model = 16 # Embedding dimensions
positional_embeddings = get_positional_encoding(max_seq_len, d_model)
# Plot positional embeddings as a heatmap
plt.figure(figsize=(10, 6))
sns.heatmap(positional_embeddings, cmap="viridis", cbar=True)
plt.title("Positional Embeddings Heatmap")
plt.xlabel("Embedding Dimensions")
plt.ylabel("Sequence Positions")
plt.show()
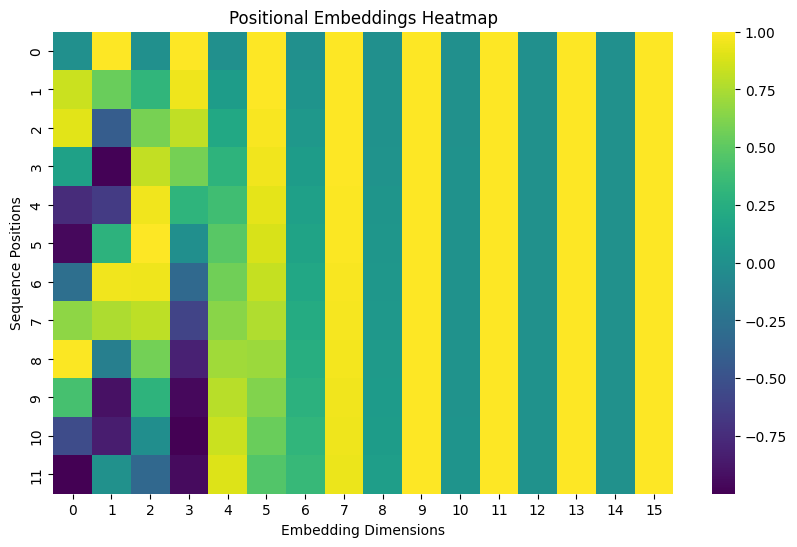
Positional Embeddings Heatmap: This visualization shows how positional information is encoded across different dimensions:
The y-axis shows sequence positions (0-11) for the sample sequence taken (same as in word embeddings plot)
The x-axis shows the embedding dimensions (0-15)
Colors represent the values of the positional embeddings:
Yellow areas represent higher positive values (closer to 1.0)
Purple areas represent lower negative values (closer to -1.0)
Green areas represent values around 0
The alternating pattern you see (waves of different colors) is characteristic of sinusoidal positional embeddings because:
Each row represents a position in the sequence
The pattern changes more slowly in earlier dimensions (left side)
The pattern changes more rapidly in later dimensions (right side)
This varying frequency helps the model distinguish between different positions in a sequence
This sinusoidal pattern is intentionally designed so that:
Each position gets a unique encoding
The relative position of tokens can be easily computed
The pattern can generalize to sequences of different lengths
Key Characteristics of Positional Embeddings:
Encode sequential order rather than semantic meaning.
Provide unique representations for each word position.
Alternatives to Absolute Positional Embeddings
In addition to absolute positional embeddings, there are alternatives such as relative positional encodings used in models like Transformer-XL. These approaches allow models to consider relative distances between tokens rather than their absolute positions, which can be beneficial for tasks requiring longer context handling.
4. Combining Word and Positional Embeddings
Transformer models utilize both types of embeddings:
Word Embeddings: Capture semantic meanings.
Absolute Positional Embeddings: Capture word order in sequences.
How They Are Combined: In most cases, word embeddings and positional embeddings are summed element-wise before being fed into the model. This integration is crucial because it allows the model to leverage both types of information effectively.
For example:
Additionally, some models like BERT introduce special tokens for segment or sentence embeddings that further enrich contextual understanding.
Conclusion
The integration of word embeddings with absolute positional embeddings enables Transformer models to process language effectively by understanding both semantic content and structural information. This dual representation is critical for modern NLP models' success across various language understanding and generation tasks. By exploring alternatives like relative positional encodings and discussing limitations of sinusoidal approaches, we gain a more comprehensive view of how these techniques contribute to advancements in NLP.
Thanks for reading till end :)